Rozwinięcie zagdanień

1. Ruch jednostajny prostoliniowy

W ruchu prostoliniowym, zwrot prędkości nie zmienia się a długość wektora przesunięcia jest równa przebytej drodze. Wartość prędkości (szybkość) V można wtedy obliczyć dzieląc drogę s przez czas t, w którym ta droga została przebyta.

Jednostką prędkości jest 1 m/s. Ciało porusza się z prędkością 1 m/s, jeżeli  drogę 1 metra przebędzie w ciągu 1 sekundy.

Wykres prędkości od czasu w ruchu jednostajnym prostoliniowym

Ponieważ prędkość w ruchu jednostajnym, prostoliniowym nie zmienia się, wykresem zależności prędkości od czasu dla ruchu jednostajnego jest prosta równoległa do osi czasu.

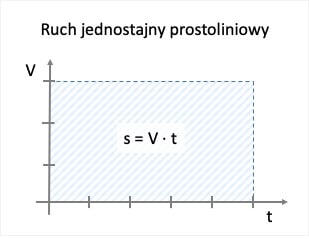
Wyliczając ze wzoru na prędkość drogę otrzymujemy s = V ⋅ t. Tym samym wzorem możemy wyrazić pole prostokąta pod wykresem zależności prędkości od czasu – pole to odpowiada przebytej drodze.

Droga w ruchu jednostajnym prostoliniowym

W ruchu jednostajnym prostoliniowym ciało w jednakowych odcinkach czasu przebywa jednakową drogę. Droga ta jest proporcjonalna do czasu trwania ruchu.

Przykład: Jeżeli pociąg porusza się ruchem jednostajnym prostoliniowym z stałą prędkością 60 km/h to w czasie 1 godziny pokona 60 kilometrów, w ciągu 2 godzin 120 kilometrów i tak dalej.

Czas [h]	Prędkość [km/h]	Droga [km]
1	60	60
2	60	120
3	60	180
4	60	240
5	60	300

Wykres drogi od czasu w ruchu jednostajnym prostoliniowym

Wykres zależności drogi od czasu dla ruchu jednostajnego prostoliniowego to linia prosta o nachyleniu odpowiadającym prędkości ciała będącego w ruchu. Im większa prędkość ciała tym większe będzie nachylenie prostej (bardziej stroma będzie prosta).

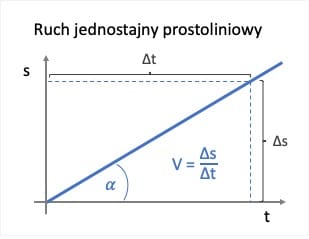
Zauważmy, że wykres ten przedstawia funkcję liniową: s = V ⋅ t. Dla funkcji liniowej nachylenie jest określone przez współczynnik kierunkowy prostej – w tym przypadku V.

Nachylenie prostej czyli prędkość możemy opisać matematycznie jako stosunek zmiany wartości na osi Y (w tym przypadku s) to zmiany wartości na osi X ( w tym przypadku t) dla dwóch dowolnych punktów prostej.

$$\Large V = \frac{\Delta s}{\Delta t}$$

W trygonometrii ten stosunek nazywany jest tangensem. Prędkość zależy od zmiany drogi w czasie – czyli jest jego pochodną. Nachylenie krzywej (tangens) jest równe wartości jej pochodnej.

2. Siły bezwładności

Siła bezwładności, a druga zasada dynamiki Newtona

W układach inercjalnych obowiązuje "normalna" postać II zasady dynamiki Newtona

 (podstawowa wersja)

Uwaga: tutaj zamiast zwykłego F napisałem specjalnie F_{oddziaływań}, aby podkreślić fakt, że "prawdziwe" siły są efektem oddziaływania (patrz rozdział Siła)i tylko dla nich obowiązuje "normalna" 2 zasada dynamiki. Za chwilę jednak powiemy o możliwości wprowadzenie "pseudo-sił", które rozszerzą zakres stosowania tego II zasady dynamiki.

A w układach nieinercjalnych?

W układach nieinercjalnych nie obowiązuje!

Dlaczego?
- bo w układach nieinercjalnych (bez żadnego powodu w postaci oddziaływania z jakimś ciałem) pojawia się sztuczna, pozorna siła bezwładności, która "psuje" to równanie.

Siła bezwładności jako poprawka do wzoru II zasady dynamiki

Można jednak poprawić (można by też zamiast "poprawić", przychylić się do słówka "oszukać") opis układów nieinercjalnych tak, aby obowiązywała w nich zmodyfikowana wersja II zasady dynamiki (zamiast "zmodyfikowana", można by w pewnym sensie powiedzieć "oszukana"). W tym celu do rzeczywistych sił (a więc sił wynikających z oddziaływań) trzeba dodać "pseudosiłę" - siłę bezwładności. 
Ta "poprawka" do naszego równania z siłami zrównoważy wpływ dodatkowego przyspieszenia związanego z układem odniesienia i wtedy wszystko zacznie się zgadzać.

Wzór na siłę bezwładności

Siła bezwładności jest równa:

Minus we wzorze bierze się z faktu, że siła bezwładności działa przeciwnie do przyspieszenia układu nieinercjalnego.

Teraz możemy wprowadzić poprawioną (obowiązującą również w układach nieinercjalnych) II zasadę dynamiki Newtona. 
Do sił rzeczywistych (wynikających z oddziaływań) dodajemy siłę bezwładności, by otrzymać zastępczą siłę wypadkową, która "uratuje" nam II zasadę dynamiki Newtona po przejściu do układu nieinercjalnego

F_całkowita = F_{oddziaływań} + F_{bezwładności}

II zasada dynamiki w układach nieinercjalnych

A oto wzór zmodyfikowanej II zasady dynamiki (z poprawką na nieinercjalność układu):

I ta poprawiona wersja II zasady dynamiki Newtona dopiero teraz dobrze działa w układach nieinercjalnych.

Na koniec możemy jeszcze nazwać sobie sumę siły wypadkowej oddziaływań i siły bezwładności nazywamy siłą całkowitą i oznaczymy (tradycyjnie) przez F, to będziemy mogli w zgodzie z prawdą wypisać taki sam wzór jak w standardowej II zasadzie dynamiki Newtona:

Tutaj F jest siłą całkowitą, 
m - masą ciała, 
a - jest przyspieszeniem ciała w układzie nieinercjalnym.

Przykłady siły bezwładności

Siły bezwładności pojawiają się w różnych sytuacjach. Oto przykłady:

	Siła bezwładności podczas ruszania pojazdu - gdy samochód rusza do przodu siła bezwładności wciska pasażerów w fotel
	Siła bezwładności podczas hamowania pojazdu - gdy samochód (lub inny pojazd) nagle hamuje, wtedy siła bezwładności rzuca pasażerem do przodu
	Siła odśrodkowa - gdy siedzimy na wirującej karuzeli siła bezwładności (nazywana w tym przypadku "siłą odśrodkową") wypycha nas i przedmioty przez nas trzymane na zewnątrz okręgu.
	Siła Coriolisa - siła ta jest nieco podobna do siły odśrodkowej i pojawia się, gdy opisujemy ruch ciała z poziomu obracającego się układu odniesienia

Chciałbym tu jeszcze raz podkreślić, że:
-  siła odśrodkowa jest siłą bezwładności 
czyli, że jest ona siłą pozorną, nie wynikającą z nowych, realnych oddziaływań.

 Siłą rzeczywiście działającą na ciało jest siła dośrodkowa, która zakrzywia tor ciała zmuszając je do krążenia po okręgu, a nie poruszania się prostoliniowo. Siła dośrodkowa wynika z istnienia jakiegoś oddziaływania -np. zaczepienia na lince, tarcia, siły grawitacji.

Jeszcze jednym istotnym spostrzeżeniem na temat sił bezwładności jest to, że jeśli układ odniesienia jest związany z jakimś obiektem materialnym (pojazdem, karuzelą itp.), to każdej sile bezwładności zawsze towarzyszy jakaś siła oddziaływań, która nadaje temu obiektowi przyspieszenie.